Entidades como la Banca March o Ibercaja Banco, entre otras, utilizan una fórmula de cálculo de los intereses a pagar de las cuotas hipotecarias que considera que el año tiene 360 días, no 365. Esta suposición provoca que la cuota de intereses sea mayor a la que correspondería de aplicar el sistema de amortización de cuota constante normal.
Si tienes una hipoteca con una cláusula del tipo “La fórmula utilizada para obtener a partir del tipo de interés anual, el importe absoluto de los intereses devengados en cada vencimiento, es la siguiente: Capital entregado o dispuesto x Tipo de interés nominal anual x Periodos de cálculo en días / 36.000. El número de días que se considerará que tiene el año para el cálculo de los intereses devengados durante períodos inferiores a un año, es de 360 días”, has pactado una condición que te perjudica y te recomendamos solicites información a nuestros economistas y abogados para saber las opciones jurídicas que tienes para reclamar al banco. Rellena nuestro formulario de contacto, sin compromiso.
Antonio Yago Ortega, notario de Murcia, analiza la fórmula de cálculo de la hipoteca con cláusula 360 en este interesante artículo. Explica el notario que en algunas escrituras de hipoteca con cláusula 360 se establecen dos fórmulas de matemática financiera incongruentes entre sí. Por una parte, la fórmula para calcular la cuota mensual de una hipoteca que se amortiza mediante el sistema francés:
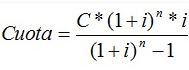
Y por otra la siguiente fórmula, utilizada para calcular la cuota de intereses correspondiente, que sumándose a la cuota de amortización, arroja la cuota mensual anterior:
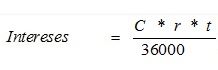
Cuando la fórmula correcta para calcular estos intereses sería:
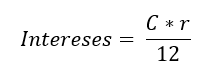
Indice
Ejemplo real de una hipoteca con cláusula 360
Cuadro de amortización normal: sistema de amortización francés
Utilizando los datos del ejemplo del notario y un sistema de amortización francés normal, resulta:
| Mes | Tipo nominal | Cuota | Amortización | Intereses | Deuda pendiente |
| 673.070 € | |||||
| 10/03/2017 | 3,00% | 3.803 € | 2.120 € | 1.683 € | 670.950 € |
| 10/04/2017 | 3,00% | 3.803 € | 2.125 € | 1.677 € | 668.825 € |
| 10/05/2017 | 3,00% | 3.803 € | 2.131 € | 1.672 € | 666.694 € |
| 10/06/2017 | 3,00% | 3.803 € | 2.136 € | 1.667 € | 664.558 € |
| 10/07/2017 | 3,00% | 3.803 € | 2.141 € | 1.661 € | 662.417 € |
| 10/08/2017 | 3,00% | 3.803 € | 2.147 € | 1.656 € | 660.270 € |
| 10/09/2017 | 3,00% | 3.803 € | 2.152 € | 1.651 € | 658.118 € |
| 10/10/2017 | 3,00% | 3.803 € | 2.157 € | 1.645 € | 655.960 € |
| 10/11/2017 | 3,00% | 3.803 € | 2.163 € | 1.640 € | 653.798 € |
| 10/12/2017 | 3,00% | 3.803 € | 2.168 € | 1.634 € | 651.629 € |
| 10/01/2018 | 3,00% | 3.803 € | 2.174 € | 1.629 € | 649.456 € |
| 10/02/2018 | 3,00% | 3.803 € | 2.179 € | 1.624 € | 647.276 € |
| Suma | 45.633 € | 25.794 € | 19.839 € |
La fórmula para calcular la cuota mensual en Excel es: =+PAGO(3,00%/12;234;-673070,30)
Y para calcular la cuota de intereses: Deuda pendiente mes anterior*3,00%/12. La amortización se obtiene de la diferencia entre la cuota mensual y la cuota de intereses, ya que:
- Cuota mensual = Cuota de amortización + Cuota constante.
El hipotecado habría pagado 45.633€ en un año y habría reducido la deuda pendiente en 25.794€.
Cuadro de amortización de una hipoteca con cláusula 360
Veamos el ejemplo que pone el notario y qué efecto tiene utilizar la fórmula de cálculo en una hipoteca con cláusula 360, teniendo en cuenta que el interés que toma el banco parte del siguiente supuesto:
Dado que considera que el año tiene 360 días, el tipo nominal que toma no es el 3%, sino el que surge de la siguiente regla de tres:
Si el tipo nominal para 360 días es un 3%, para 365 (366 los años bisiestos) es: 3%*365,25/360 = 3,04375%. En otras palabras, toma un interés superior al comunicado al cliente. Por otro lado, la fórmula para calcular la cuota de interés también se altera, siendo en Excel la cuota de interés del mes de marzo de 2017: =+(G37*3%*(B38-B37))/360, dónde G37 es la deuda pendiente del mes anterior y (B38-B37) los días naturales del 10/02/2017 al 10/02/2017. El cuadro de amortización de la hipoteca con cláusula 360 sería:
| Mes | Tipo nominal | Cuota | Amortización | Intereses | Deuda pendiente |
| 10/02/2017 | 673.070 € | ||||
| 10/03/2017 | 3,04375% | 3.817 € | 2.247 € | 1.570 € | 670.823 € |
| 10/04/2017 | 3,04375% | 3.817 € | 2.085 € | 1.733 € | 668.739 € |
| 10/05/2017 | 3,04375% | 3.817 € | 2.146 € | 1.672 € | 666.593 € |
| 10/06/2017 | 3,04375% | 3.817 € | 2.095 € | 1.722 € | 664.498 € |
| 10/07/2017 | 3,04375% | 3.817 € | 2.156 € | 1.661 € | 662.342 € |
| 10/08/2017 | 3,04375% | 3.817 € | 2.106 € | 1.711 € | 660.235 € |
| 10/09/2017 | 3,04375% | 3.817 € | 2.112 € | 1.706 € | 658.123 € |
| 10/10/2017 | 3,04375% | 3.817 € | 2.172 € | 1.645 € | 655.951 € |
| 10/11/2017 | 3,04375% | 3.817 € | 2.123 € | 1.695 € | 653.828 € |
| 10/12/2017 | 3,04375% | 3.817 € | 2.183 € | 1.635 € | 651.645 € |
| 10/01/2018 | 3,04375% | 3.817 € | 2.134 € | 1.683 € | 649.511 € |
| 10/02/2018 | 3,04375% | 3.817 € | 2.140 € | 1.678 € | 647.372 € |
| Suma | 45.810 € | 25.699 € | 20.111 € |
El cliente habría pagado 45.810€ (176€ más) y su deuda pendiente se habría reducido en 25.699€ (95€ menos). El perjuicio en el ejemplo de un solo año son 81€.
